Logic theories and deductive inference (syllogism) as Artificial Intelligence tools

1. Introduction

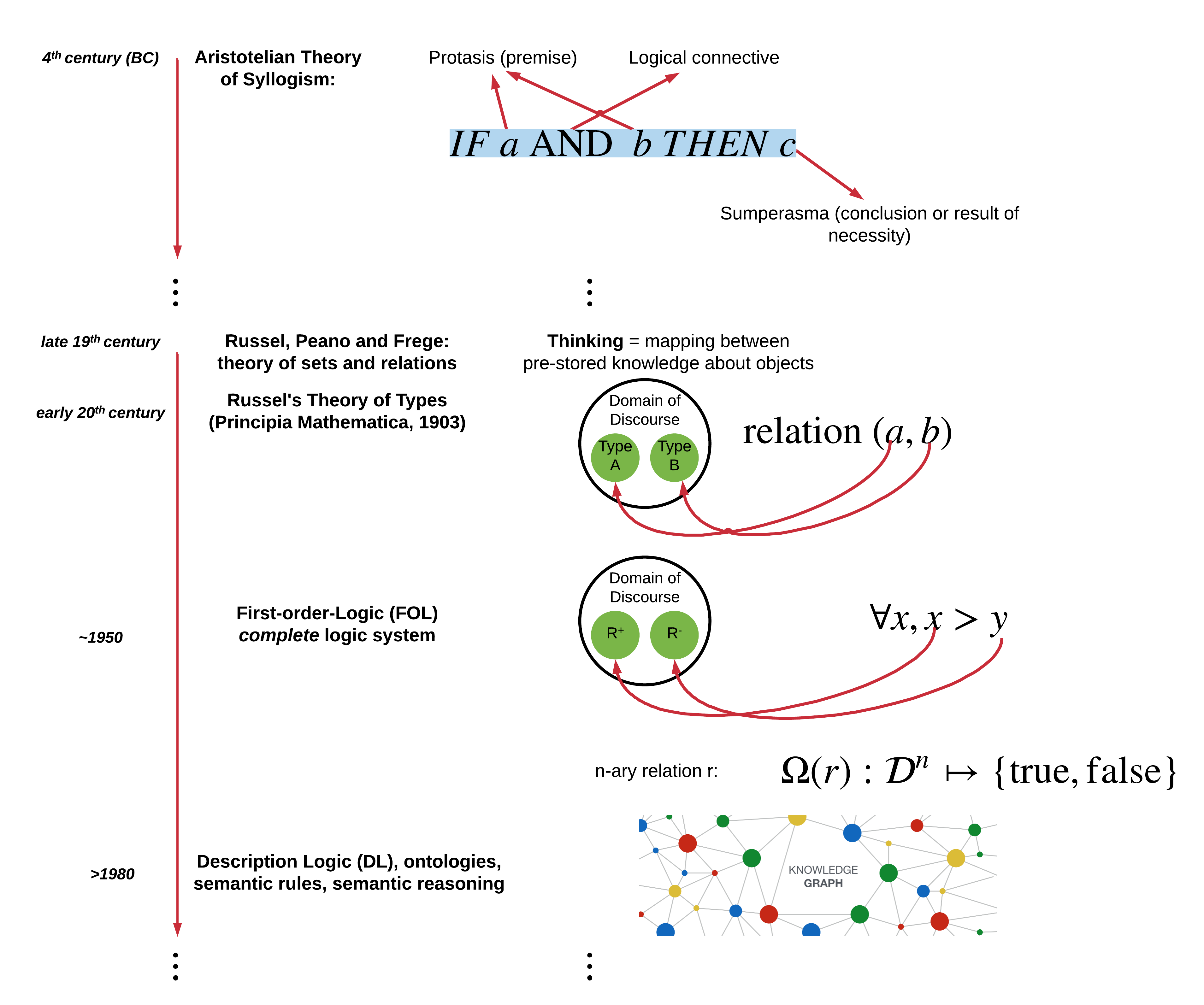
The study of "Logic" has its roots in the Aristotelian theory of syllogism (deduction) [1]. According to Aristotle, a syllogism is "speech (logos) in which certain things have been supposed, different from those supposed results of necessity because of their being so". The "things supposed" comprise the premise (protasis), while the "results of necessity" comprise the conclusion (sumperasma), that is, the logical consequence. For instance, a statement $C$ is the consequence (result of necessity) of the fact that $A$ and $B$ being true (they are supposed), if its logical truthfulness cannot be challenged given the truthfulness of the things supposed.  

The Aristotelian theory of logic had remained dominant until the mid 19th century, followed by approximately one hundred years of research that led to the conception of "modern logic". During that transformation time, G.E. Moore and B. Russel had put effort in formalising logic by referring to "common sense" [2][3], then they started adding bounds and discussing the "set theory" as the foundations for mathematics. During early twentieth century, the bounds became narrower following the realisation of the "paradoxes of logic" and the work of B. Russel on "Types theory". These led to the establishment of "First-Order Logic (FOL)", otherwise called the "modern logic", which had not happened before the mid 20th century [4].

2. The road towards modern logic

During the second half of the 19th century, logic was studied within the framework of the classical philosophy, as well as in relation with the science of mathematics; algebra, axiomatics and analysis. Since the late 19th century the theory of logic started becoming a blend of the propositional and predicate logic (http://www.iep.utm.edu/prop-log/) on one hand and the theory of sets and relations on the other hand. At that time, “thinking” was considered the ability of mind to relate between “things”, i.e., derive conclusions about properties of certain things based on knowledge about properties of other things. This process of “thinking”, performed by the mind, is essentially a mapping between pre-stored knowledge about things. Based on this understanding, B. Russell [5] formed the “symbolic logic” within the areas of “calculus of propositions”, “calculus of classes” and “calculus of relations”. B. Russel, together with Peano and Frege agreed in their separate works that mathematics were actually “symbolic logic”, i.e., the symbols are used to help expressing logical propositions and relations between things.

More specifically, at the beginning of the 20th century, the work of Russell, Peano and Frege considered the logical systems within the bounds of the theory of sets. They had believed in the principle of “comprehension”, meaning that a thing/object could be fully described by certain attributes, properties, qualities, etc. However, later this theory faced certain contradictions (or paradoxes or antinomies), with the most significant being the “Russell’s paradox”, which was formulated in terms of notions of the set theory itself, i.e. the notion of negation and membership. The discovery of the paradoxes, led to the revision of the foundations of set-theory and its effect on logic and mathematics.

In order to resolve the issues revealed by the paradoxes, Russell developed his “Theory of Types”, which was incorporated into his work on “Principia Mathematica”, co-authored with Whitehead [5]. The theory of types [6] introduced the notion of “types” of elements of a set. This way, the notion of “comprehension” was preserved. According to van der Waerden, in his Moderne Algebra [7], the “Theory of Types” was then the most important system of logic. However, in 1931, Godel announced his first “incompleteness theorem” [8]. During that time (1930), the early work of Skolem [9] on the Zermelo system and the work of Von Neumann on his logic system [10], led to the appearance of “First Order Logic (FOL)” as the basic system for logic. Hilbert & Ackermann’s “Grundzuge der theoretischen Logik” [11] shows that FOL was studied as a separate system of logic by around 1928. This book shows also that the use of higher-order logic would be possible and necessary when one would require to analyse meta-concepts of mathematics.

FOL was adopted as the natural system of logic by 1950, adhering to:

i) The principle of deduction (conditions of arguments to be correct following analysis of their validity);

ii) The principle of universality (logical sentences formed independently of specific topic);

iii) The “Kant’s principle” (study the formulation of arguments and deductions using logical variables and not instantiations within a domain of discourse;

iv) The Leibnizian ideal (compute logical deductions with machine algorithms).

The latter was first achieved by Boole with his algebra of logic. Then, Frege made an impressive step forward and Godel followed by establishing certain implementation limitations.

The concept “domain of discourse” was defined by G. Boole in 1854 in his work “Laws of Thought”, as:

“In every discourse, whether of the mind conversing with its own thoughts, or of the individual in his intercourse with others, there is an assumed or expressed limit within which the subjects of its operation are confined. The most unfettered discourse is that in which the words we use are understood in the widest possible application, and for them the limits of discourse are co-extensive with those of the universe itself. But more usually we confine ourselves to a less spacious field. Sometimes, in discoursing of men we imply (without expressing the limitation) that it is of men only under certain circumstances and conditions that we speak, as of civilized men, or of men in the vigour of life, or of men under some other condition or relation. Now, whatever may be the extent of the field within which all the objects of our discourse are found, that field may properly be termed the domain of discourse...”

In summary, it can be deduced that around 1900 logic was conceived as a theory of sentences, sets and relations; almost until 1930 the established logic system was (simple) type theory, while by 1950 FOL became the paradigm logical system.

3. First Order Logic

In general, a first-order language system assigns variable symbols to logical constants. The language also defines the "domain of discourse", which specifies the range of the variables, in line with the Russel's Theory of Types. Sentences written using such languages have clear semantics. For instance, assume the domain of discourse $\mathcal{D}$, being a set of objects of a certain type. An example of a first-order statement within this domain could be the $ x,a(x)$, stating that some logical sentence $x$ is true and at the same time it's logical transformation through the predicate $a(x)$ is also true. If a domain of discourse is not clearly defined, the logical derivations may not be always feasible. For instance, the sentence $\forall x, x > y$ cannot be logically interpreted without knowing the domains of the logical variables $x$ and $y$. So, if $x$ and $y$ are real numbers, the statement is false because there are real numbers that can be greater than other real numbers. But, if $x$ is a positive number and $y$ is a negative number, the statement becomes always true since all positive numbers are greater than any negative number. Moreover, assuming $\mathcal{D}$ being the domain of building zones, we can define the adjacency of two building zones as a binary predicate $a(\cdot)$, taking two building zones are arguments and returning $\top$ if the two zones are indeed adjacent or $\bot$ if they are not.

If the validity or not of any given sentence can always be deduced through some language system, then this language is said to be "complete". According to Godel, the FOL language system is complete, although mathematical systems cannot guarantee in general syntactic and semantic completeness [8]. This understanding made FOL a sufficient language for codifying mathematical proofs. Moreover, the tools utilised in mathematical proofs (theorems, sentences, etc.) can be explicitly supported by quantification expressions such as the: "given any", "there is", "for any", "for each". For instance, one can write a sentence like: $\forall{x}(a(x) \mapsto b(x))$ .

Summarizing, to guarantee completeness, a FOL language always needs to define a "domain of discourse" $\mathcal{D}$, also defining the classes $\Omega$ of all terms used in the language. For instance, an $n$-ary relation $r$ is essentially a mapping of the form $\Omega(r)$: $\mathcal{D}^{n} \mapsto \{ \mathrm {true,false} \}$. That is, a statement is true if it can be inferred by some logical deduction within the domain $\mathcal{D}$. In mathematics, a formula is logically valid only if it is true no matter the instantiation of the variables in the defined domain of discourse. Certain "axioms" can be also defined within a domain of discourse, as being true anyway and helping the inference.

4. Syllogism - Deductive Inference Systems

Basic systems of "Logic" deal with certain logical "statements" or "sentences" being true or false. The logical statements under consideration are typically called "propositions" (see also the terms "propositional logic" or "sentential logic" or even "zero-order logic"). Logical statements can be combined using "logical connectives". For instance, the "and" (conjunction), the "or" (disjunction), the "not" (negation) and the "if" (denoting condition of existence) are logical connectives of the English language. Moreover, "logical axioms" can be pre-defined, stating things that are believed to be true by design. A third element of logic systems are the "inference rules", which specify given knowledge about the truthfulness of combinations of propositions through logical connectives. In logic, an "inference rule" is a logical $n$-ary function that takes as input certain statements, analyzes their syntax and returns a conclusion. For example, in the  "modus ponens" inference system, an inference rule takes two inputs, one statement in the form "if $a$ then $b$" and another in the form "$a$", and returns the conclusion "$b$". A fourth element are the "quantifiers", which are operators that map propositions (their symbolic representation) to a specific domain of discourse.

It has been mentioned earlier, that according to the Kant's principle, only the form of the statements should matter and not the instances of the logical variables. We take an example of a syllogism from Aristotle: All men are speakers. No oyster is a speaker. Therefore, no oyster is a man. This example can be transformed to the first-order sentence: $\forall a,b(a)$. $\not b(c)$. Therefore, $a \ne c$. Another example would be:

• Statement 1: Presence of people in a closed room without any other sources of CO2, causes CO2 to increase.
• Statement 2: There are no people in the room.
• Deduction: The CO2 value cannot be high.

The given statements are what we know is true (knowledge facts). Other knowledge can be inferred by the given statements after applying some inference mechanism. The knowledge facts and the inference rules are considered known a-priori in deductive inference, either because they are part of the expert knowledge or because they can be derived analytically using a-priori knowledge of the system.

Therefore, the concept "Deductive Inference" is concerned with checking whether a statement is true given the truthfulness of another statement or a combination of statements through logical connectives. There are many such systems for first-order logic, including the "Hilbert-style deductive systems", the "natural deduction", the "sequent calculus", the "tableaux method", and the "resolution". It is noted that derivations of proofs in "proof theory" are essentially deductions. A deductive inference system is considered "sound" if any statement that can be derived in the system as true is logically valid. Conversely, a deductive inference system is "complete" if every logically valid statement can be derived through the system. All above mentioned deductive inference systems are both sound and complete. The conclusions in these deductive inference systems do not typically consider the semantic interpretations of the statements in a domain of discourse. On the other hand, in FOL, deductive inference is only semi-decidable, that is, if $a$ logically implies $b$ then this can be deduced by a deductive inference system. However, if $a$ does not logically imply $b$, this does not mean that $a$ logically implies $\not b$.

In general, the deductive inference systems use several logical and non-logical symbols from the alphabet, such as:

• The quantifier symbols $\forall$ and $\exists$
• The logical connectives: $\wedge$ for conjunction, $\vee$ for disjunction, $\Rightarrow$ for implication, $\Leftrightarrow$ or $\equiv$ for biconditional, $\neg$ or $\tilde{}$ for negation, etc.    
• Parentheses, brackets, and other punctuation symbols.
• An infinite set of variables, often denoted by lower-case letters at the end of the alphabet $x,y,z,\cdot$. Variables are often distinguished by sub-scripts: $x_0,x_1,x_2,\cdot$.
• An equality symbol, e.g., $=$
• The truth constants are included, e.g., $\top$ for "true" and $\bot$ for "false".
• Additional logical connectives that may be required, such as "NAND" and "exclusive OR".

On the other hand, non-logical symbols represent semantic relations, i.e. mappings of knowledge objects within a domain of discourse. In the past, FOL considered a single fixed set of non-logical symbols to apply deductive inference. The current practice, however, is to define a different set of non-logical symbols within the bounds of an application. Such definition of logical symbols can be made through "ontology languages". Ontology languages are essentially collections of a finite number of $n$-ary predicates/symbols, representing relations between $n$ objects. For example, $\text{man}(x)$ is an example of a predicate of arity 1, which defines that "$x$ is a man"; $\text{father}(x,y)$ is a predicate of arity 2, interpreted as "$x$ is the father of $y$".

For completeness, we note here that there are also other types of inference:

i) Inductive inference, where the rules are not considered known a-priori; possible rules are derived from the propositions and the observations/experiences, as if the logic system is "identified" from inputs and outputs;

ii) Abductive inference, where the observations/experiences as well as the rules are considered known, and the logically valid truths are inferred accordingly. E.g., I observe something (fault detection) and knowing how the system works I try to infer what might have caused it (fault isolation).

5. Ontology languages and Description Logic

Ontology languages allow the encoding of pre-existing or acquired data/information about a specific domain of discourse. They typically include also inference (or "reasoning") rules that help with making logical conclusions above the modeled data/information. Ontology languages are usually declarative languages and are commonly based either on FOL or on "Description Logic" (DL) [12]. DL is a family of formal knowledge representation languages, which are typically subsets of FOL (less expressive than FOL). They are used to represent a domain of discourse in a structured way, offering clear decide-ability with no gaps due to adding constraints. DLs usually use binary predicated (two-variable logic). There are enough good-quality reasoning mechanisms (decision procedures) designed and implemented for DLs.

DLs have been used as the logical formalism for "ontologies" and the "Semantic Web". For instance, the Web Ontology Language (OWL) and its profile is based on DLs [13]. In DLs usually a "unary predicate" of FOL, is called a "class", a "binary predicate" is called a "property" and a "constant" is called an "individual". DLs pose certain relationships with other logics as well. For instance, Fuzzy description logic combines fuzzy logic with DLs. Fuzzy logic deals with the notions of vagueness and uncertainty about the classes of certain logical variables. These properties are common in intelligent systems, where concepts do not have clear boundaries. Fuzzy logic therefore generalises the description logic to deal with vague concepts. In addition, the "Temporal Description Logic" allows reasoning about time dependent concepts and can be the combination of DL with a modal temporal logic such as "Linear Temporal Logic". Concluding, DLs are a very good tool for representing data and information models and inference rules, and subsequently inferring mappings and values from known facts, i.e. generating knowledge.

We make use of ontologies and inference rules in our innovative SEMIoTICS architecture which is part of our $\text{Domognostics}^{TM}$ product in the smart buildings domain.

Schematic Summary

References

[1] S. Robin, "Aristotle’s Logic," in The Stanford Encyclopedia of Philosophy, winter 2016 ed., E. N. Zalta, Ed. Metaphysics Research Lab, Stanford University, 2016.
[2] G. E. Moore, "A Defence of Common Sense," in Contemporary British Philosophy (2nd series), J. H. Muirhead, Ed. Allen and Unwin, London, 1925, pp. 192–233.
[3] B. Russell, Common Sense and Nuclear Warfare, 1st ed. Routledge, Oxford, UK, May 2001.
[4] J. Ferreiros, "The road to modern logic-an interpretation," Bulletin of Symbolic Logic, vol. 7, no. 4, pp. 441–484, 12 2001. [Online]. Available: http://projecteuclid.org/euclid.bsl/1182353823
[5] B. Russell, Ed., The principles of mathematics. Cambridge University Press, 1903, (2nd edition 1937). Reprint London, Allen and Unwin, 1948.
[6]    B. Russel, "Mathematical logic as based on the theory of types," American Journal of Mathematics, vol. 30, pp. 222–262, 1908.
[7] B. L. V. der Waerden, Ed., Moderne Algebra.    Springer, Berlin, 1930.
[8] K. Godel, "Über formal unentscheidbare sätze der principia mathematica und verwandter systeme i," Monatshefte für Math. u. Physik, vol. 38, pp. 173–198,
1931.
[9] T. Skolem, "Einige bemerkungen zur axiomatischen begriindung der mengenlehre," Dem Femte skandinaviska mathematikerkongressen, Akademiska Bokhandeln, 1923, helsinki.
[10] J. V. Neumann, "Eine axiomatisierung der mengenlehre," Journal fur die reineund angewandte Mathematik, vol. 154, pp. 219–240, 1925, reprint in Collected Works, vol. 1, Oxford, Pergamon, 1961.
[11] W. A. David Hilbert, Ed., Grundzuge der theoretischen Logik. Springer, Berlin, 1928, (2nd edition 1937). Reprint London, Allen and Unwin, 1948.
[12] F. Baader, D. Calvanese, D. L. McGuinness, D. Nardi, and P. Patel-Schneider, Eds., The Description Logic Handbook. Cambridge University Press, 2003.
[13] P. P.-S. I. Horrocks, "Reducing owl entailment to description logic satisfiability," In Proc. of the 2nd International SemanticWeb Conference (ISWC), 2003, http://www.cs.man.ac.uk/ horrocks/Publications/download/2003/HoPa03c.